Python Covariance and Correlation: Unlocking Insights and Patterns.

The covariance between two random variables measures the degree to which the two variables move together – it captures the linear relationship.

Interpreting covariance is simple: if the value is high, then the two variables are positively related, that is, if one variable increases, the other variable also increases. On the other hand, if the value is negative, then the two variables are inversely related, that is, if one variable increases, the other variable decreases.

Properties of covariance:
▪ positive covariance: variables move together
▪ negative covariance: variables move in opposite directions
▪ covariance of variable with itself == variance

Pitfalls of covariance:
▪ actual value of covariance not meaningful
▪ can range from minus to plus infinity
▪ squared units

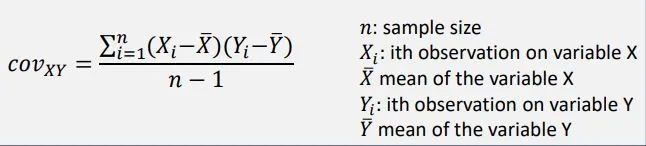
The correlation coefficient (r) measures the strength of the linear relationship (correlation) between two variables. It´s the standardized covariance and is easier to interpret as values are between -1 and +1.

There are two types of correlation: positive and negative. Positive correlation means that as one variable increases, so does the other. For example, the more you study, the higher your grades will be. Negative correlation means that as one variable increases, the other decreases. For instance, the more junk food you eat, the worse your health will be.

R(xy) = (𝑐𝑜𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒 𝑜𝑓 𝑋 𝑎𝑛𝑑 𝑌) / ((𝑠𝑎𝑚𝑝𝑙𝑒 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑋)(𝑠𝑎𝑚𝑝𝑙𝑒 𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 𝑜𝑓 𝑌))

Correlation Coefficient (r) Interpretation:
r = 1 - perfect positive correlation
0 < r < 1 - Positive linear relationship
r = 0 - no linear relationship
-1 < r < 0 - negative linear relationship
r = -1 - perfect negative correlation

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

N = 66

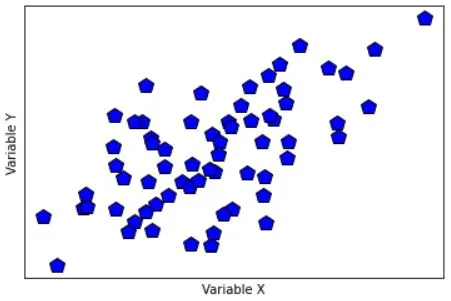
# generate correlated data
x = np.random.randn(N)
y = x + np.random.randn(N)

# plot the data
plt.plot(x,y,'kp',markerfacecolor='b',markersize=12)
plt.xlabel('Variable X')
plt.ylabel('Variable Y')
plt.xticks([])
plt.yticks([])
plt.show()

## compute covariance

# precompute the means
meanX = np.mean(x)
meanY = np.mean(y)

### the loop method
covar1 = 0
for i in range(N):
    covar1 = covar1 + (x[i]-meanX)*(y[i]-meanY)
    

# and now for the normalization
covar1 = covar1/(N-1)

### the linear algebra method
xCent = x-meanX
yCent = y-meanY
covar2 = np.dot(xCent,yCent) / (N-1)

### the Python method
covar3 = np.cov(np.vstack((x,y)))

print(covar1,covar2,covar3)

OUT:
0.9609676940493194 0.9609676940493196 [[1.03431923 0.96096769] [0.96096769 2.32630356]]

## now for correlation

### the long method
corr_num = sum( (x-meanX) * (y-meanY) )
corr_den = sum((x-meanX)**2) * sum((y-meanY)**2)
corr1 = corr_num/np.sqrt(corr_den)


### the Python method
corr2 = np.corrcoef(np.vstack((x,y)))

print(corr1,corr2)

OUT:
0.6195099623133035 [[1. 0.61950996] [0.61950996 1. ]]

r,p = stats.pearsonr(x,y)
print(r,p)

OUT:
0.6195099623133037 2.926584255137327e-08

So there you have it – a comprehensive breakdown of covariance and correlation in statistics, explained in a way that's both easy-to-understand and entertaining to read. With Python and its data analysis libraries, we can easily implement these statistical concepts into our work and achieve more meaningful insights. So go ahead, try implementing these techniques in your own projects and see the results for yourself. Happy analyzing!