Drawing fractals.
In this section we will deal with fractals, and let me remind you that a fractal is a geometric shape with a repeating structure at different scales, e i a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole. Many fractals appear similar at various scales, which is called self-similarity. Latin word frāctus means "broken" or "fractured".

Python Knowledge Base: Make coding great again.
- Updated:
2025-07-03 by Andrey BRATUS, Senior Data Analyst.
Drawing snowflake fractal:
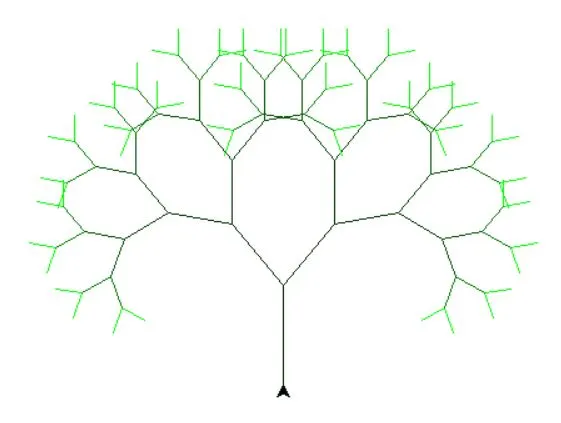
Drawing tree fractal:
Drawing stars fractal:
Drawing H recursion fractal:
Drawing Sierpiński triangle with Python:
Python can handle repeating structure at different scales applying a recursive solution.
The drawing part will be handeled by Turtle graphics, which was part of the original Logo programming language developed by Wally Feurzeig, Seymour Papert and Cynthia Solomon in 1967.
Lets start with simple example of snowflake fractal made of snowflake pattern made of snowflake pattern.
from turtle import *
def koch_flake(length, order):
if(order == 0):
forward(length)
return
koch_flake(length/3,order-1)
left(60)
koch_flake(length/3, order - 1)
right(120)
koch_flake(length/3, order - 1)
left(60)
koch_flake(length/3,order-1)
def draw_flake():
speed('fastest')
up()
backward(200 / 2.0)
down()
col = ["red", "purple", "yellow", "cyan"]
fillcolor("black")
begin_fill()
for i in range(3):
color(col[i])
koch_flake(300.0, 4)
left(-120)
color(col[i+1])
end_fill()
mainloop()
draw_flake()

Another classical fractal example is drawing a tree. speed() is used to define the speed of the pen and pencolor() is used for setting color according to color level.
from turtle import *
import turtle
speed('fastest')
right(-90)
angle = 40
def yaxis(size, lvl):
if lvl > 0:
colormode(255)
pencolor(0, 255 // lvl, 0)
forward(size)
right(angle)
yaxis(0.8 * size, lvl - 1)
pencolor(0, 255 // lvl, 0)
lt(2 * angle)
yaxis(0.8 * size, lvl - 1)
pencolor(0, 255 // lvl, 0)
right(angle)
forward(-size)
yaxis(80, 7)
turtle.done()
Lets proceed with simple example of stars fractal made of stars pattern made of stars pattern.
from turtle import *
import turtle
tur = turtle.Turtle()
tur.speed('fastest')
tur.getscreen().bgcolor("purple")
tur.color("pink")
tur.penup()
tur.goto((-200, 50))
tur.pendown()
def star(turtle, size):
if size <= 10:
return
else:
for i in range(5):
turtle.forward(size)
star(turtle, size / 3)
turtle.left(216)
star(tur, 360)
turtle.done()

Recursion is the process of repeating items in a similar way and fractal is used to generate an infinite amount of copies of pictures that form a fractal pattern.
from turtle import *
import turtle
speed = 5
bg_color = "purple"
pen_color = "pink"
screen_width = 800
screen_height = 800
drawing_width = 700
drawing_height = 700
pen_width = 7
title = "python-code.pro"
fractal_depth = 3
def drawline(tur, pos1, pos2):
tur.penup()
tur.goto(pos1[0], pos1[1])
tur.pendown()
tur.goto(pos2[0], pos2[1])
def recursivedraw(tur, x, y, width, height, count):
drawline(
tur,
[x + width * 0.25, height // 2 + y],
[x + width * 0.75, height // 2 + y],
)
drawline(
tur,
[x + width * 0.25, (height * 0.5) // 2 + y],
[x + width * 0.25, (height * 1.5) // 2 + y],
)
drawline(
tur,
[x + width * 0.75, (height * 0.5) // 2 + y],
[x + width * 0.75, (height * 1.5) // 2 + y],
)
if count <= 0: # The base case
return
else: # The recursive step
count -= 1
recursivedraw(tur, x, y, width // 2, height // 2, count)
recursivedraw(tur, x + width // 2, y, width // 2, height // 2, count)
recursivedraw(tur, x, y + width // 2, width // 2, height // 2, count)
recursivedraw(tur, x + width // 2, y + width // 2, width // 2, height // 2, count)
if __name__ == "__main__":
screenset = turtle.Screen()
screenset.setup(screen_width, screen_height)
screenset.title(title)
screenset.bgcolor(bg_color)
artistpen = turtle.Turtle()
artistpen.hideturtle()
artistpen.pensize(pen_width)
artistpen.color(pen_color)
artistpen.speed(speed)
recursivedraw(artistpen, - drawing_width / 2, - drawing_height / 2, drawing_width, drawing_height, fractal_depth)
turtle.done()

In mathematics, the term chaos game originally referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it.
The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal attractive fixed set with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. This is one of the classical examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but to be honest was known as a decorative pattern many centuries before the work of Sierpiński.
import turtle
tur = turtle.Turtle()
tur.speed('fastest')
tur.getscreen().bgcolor("purple")
tur.color("pink")
def sier(side, level):
if level == 1:
for i in range(3):
turtle.fd(side)
turtle.left(120)
else:
sier(side/2, level-1)
turtle.fd(side/2)
sier(side/2, level-1)
turtle.bk(side/2)
turtle.left(60)
turtle.fd(side/2)
turtle.right(60)
sier(side/2, level-1)
turtle.left(60)
turtle.bk(side/2)
turtle.right(60)
def main():
sier(200, 5)
if __name__ == '__main__':
main()
turtle.mainloop()

